Duncan's Blog

红黑树学习

Veröffentlicht am | in

1.定义

1.红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色.并且有如下性质:

  • 1)性质1. 节点是红色或黑色。

  • 2)性质2. 根节点是黑色。

  • 3)性质3 每个叶节点（null节点，空节点）是黑色的。

  • 4)性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

  • 5)性质5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

特性:从根到叶子结点最长的可能路径不多于最短的可能路径的两倍长.

2.操作

1.左旋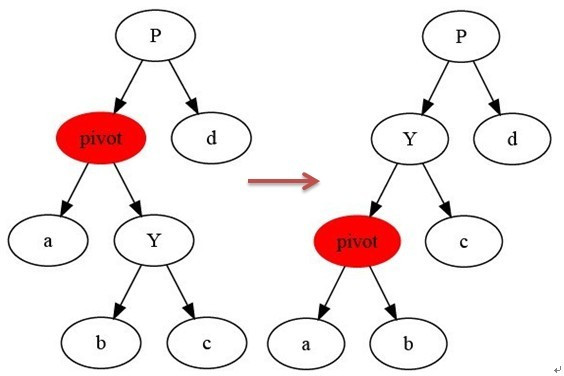
图片来自慕课

2.右旋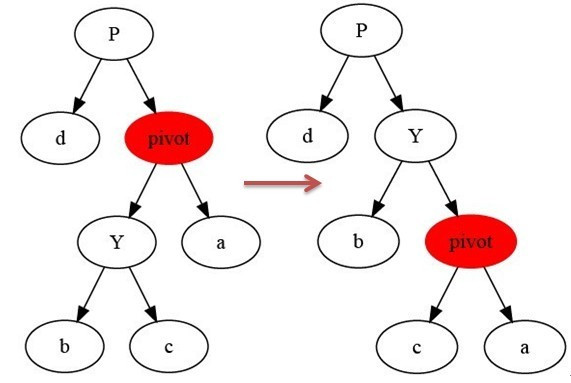
图片来自慕课

3.插入(5种情况)

  • 1)情况1:插入的是根结点
    • 对策:直接把该结点涂黑
  • 2)情况2:插入的结点的父结点是黑色
    • 对策:Do nothing
  • 3)当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色
    • 对策:将当前节点的父节点和叔叔节点涂黑，祖父节点涂红，把当前节点指向祖父节点，从新的当前节点重新开始算法。
  • 4)当前结点的父结点是红色,叔叔结点是黑色,当前结点是其父结点的右孩子
    • 对策:当前节点的父节点做为新的当前节点，以新当前节点为支点左旋。
  • 5)当前结点的父结点是红色,叔叔结点是黑色,当前结点是其父结点的左孩子
    • 对策:父节点变为黑色，祖父节点变为红色，在祖父节点为支点右旋

4.删除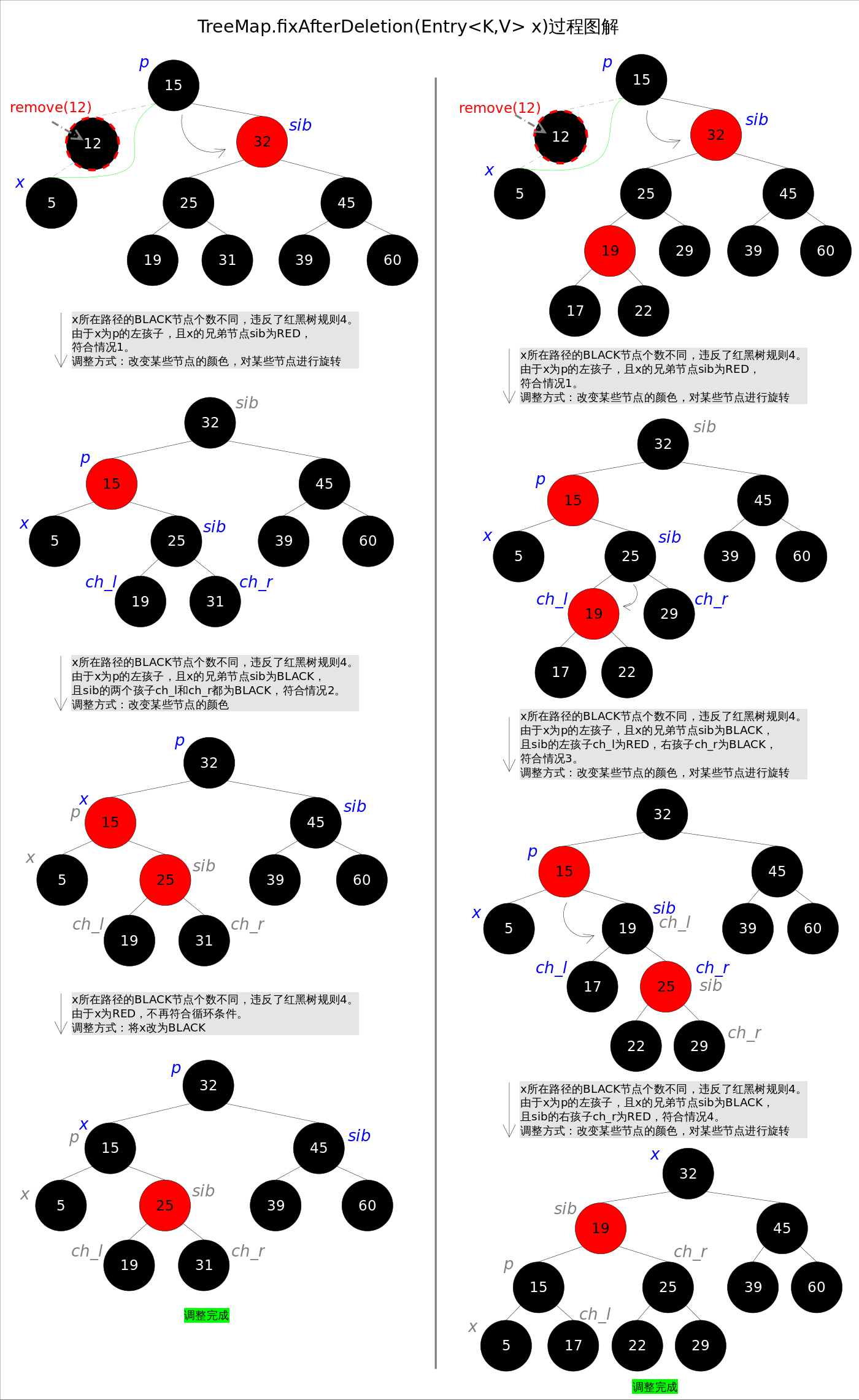
删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
private void fixAfterDeletion(Entry<K,V> x) {
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) {
            Entry<K,V> sib = rightOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // 情况1
                setColor(parentOf(x), RED);             // 情况1
                rotateLeft(parentOf(x));                // 情况1
                sib = rightOf(parentOf(x));             // 情况1
            }
            if (colorOf(leftOf(sib))  == BLACK &&
                colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);                     // 情况2
                x = parentOf(x);                        // 情况2
            } else {
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);       // 情况3
                    setColor(sib, RED);                 // 情况3
                    rotateRight(sib);                   // 情况3
                    sib = rightOf(parentOf(x));         // 情况3
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况4
                setColor(parentOf(x), BLACK);           // 情况4
                setColor(rightOf(sib), BLACK);          // 情况4
                rotateLeft(parentOf(x));                // 情况4
                x = root;                               // 情况4
            }
        } else { // 跟前四种情况对称
            Entry<K,V> sib = leftOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // 情况5
                setColor(parentOf(x), RED);             // 情况5
                rotateRight(parentOf(x));               // 情况5
                sib = leftOf(parentOf(x));              // 情况5
            }
            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);                     // 情况6
                x = parentOf(x);                        // 情况6
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);      // 情况7
                    setColor(sib, RED);                 // 情况7
                    rotateLeft(sib);                    // 情况7
                    sib = leftOf(parentOf(x));          // 情况7
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况8
                setColor(parentOf(x), BLACK);           // 情况8
                setColor(leftOf(sib), BLACK);           // 情况8
                rotateRight(parentOf(x));               // 情况8
                x = root;                               // 情况8
            }
        }
    }
    setColor(x, BLACK);
}

(具体插入和删除操作见 http://www.imooc.com/article/11715)

分享