1.走进JAVA

1.JDK(Java Developmen Kit):将Java程序设计语言,Java虚拟机和Java API类库这三部分统称为JDK.

2.JRE(Java Runtime Environment):把Java API类库中的Java SE API子集和Java虚拟机这两部分统称为JRE.

2.JAVA内存区域与内存溢出异常

先放一张jvm运行时数据区分配情况图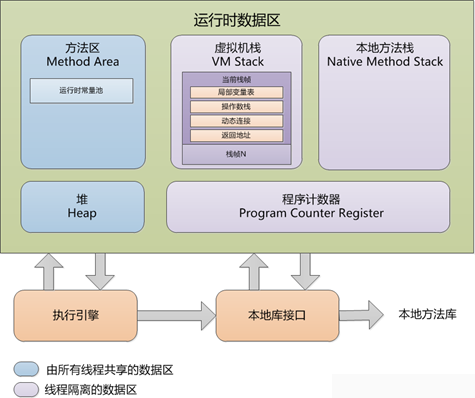

1. Java堆中分配内存方式:如果Java堆中的内存是绝对规整的,所有用过的内存都放在一边,空闲的内存放在另一边,中间放着一个指针作为分界点的指示器,那所分配内存就是仅仅把那个指针向空闲空间那边挪动一段与对象大小相等的距离,这种分配方式称为指针碰撞(Bump the pointer);如果Java堆中的内存并不是规整的,已使用内存和空闲的内存相互交错,虚拟机就必须维护一个列表,记录上哪些内存块是可用的,在分配的时候从列表中找到一块足够大的空间划分给对象,并更新列表上的记录,这种分配方式称为空闲列表(Free List);

2. 划分内存过程需要考虑同步问题,两种方式:1)对分配内存空间的动作进行同步处理(CAS配上失败重试的方式保证更新操作的原子性);2)每个线程在Java堆中预先分配一小块内存,为本地线程分配缓冲(Thread Local Allocation Buffer),当TLAB分配完了之后再做同步操作.

3. 对象的访问定位:使用句柄和直接指针

3.垃圾收集算法

• 标记-清除算法:首先标记出所有需要回收的对象,在标记完成后一次性回收所有被标记的对象.
• 复制算法:将可用内存分为两块,每次只使用其中一块,当着一块内存用完了,就将还存活的对象复制到另一块上,然后把已使用的内存空间一次清理掉.
• 标记-整理算法:首先标记出所有需要回收的对象,让所有存活的对象都向一端移动,然后直接清理掉端界外的内存.\
• 分代收集法:将堆分为新生代和老年代,根据每个代的特点选择合适的垃圾回收算法.

4.垃圾收集器

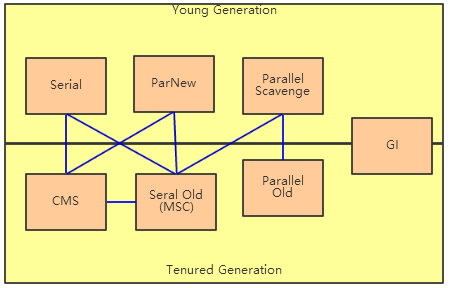
1. Serial收集器
   这个收集器是一个单线程的收集器,但它的”单线程”的意义并不仅仅说明它只会使用一个CPU或一条收集线程去完成垃圾收集工作,更重要的是在它进行垃圾收集时,必须暂停其他所有的工作线程,直到它收集结束.(Client模式下默认的垃圾收集器)

2. ParNew收集器
   ParNew收集器就是Serial收集器的多线程版本,除了使用多条线程进行垃圾收集之外,其余行为包括Serial收集器可用的所有控制参数,收集算法,Stop the world,对象分配规则,回收策略等都与Serial收集器完全一样.(Server模式下的垃圾收集器)

3. Parallel Scavenge收集器
   Parallel Scavenge收集器更多关注于控制吞吐量(吞吐量=运行用户代码时间/(运行用户代码时间+垃圾收集时间)).

4. Serial Old收集器

5. Parallel Old收集器

6. CMS收集器
   CMS收集器是一种以获取最短回收停顿时间为目标的收集器.目前很大一部分的Java应用集中在互联网站或者B/S系统的服务端上.
   CMS收集器是基于”标记-清除”算法实现的,运作过程分为4个步骤:

• 初始标记
• 并发标记
• 重新标记
• 并发清除

1. G1收集器
   运作大致分为:

• 初始标记(标记GC Roots直接关联到的对象)
• 并发标记(GC Roots可达性分析)
• 最终标记(修正在并发标记阶段标记发生改变的那部分标记记录)
• 筛选回收(对各个Region的回收价值和成本排序)

5.内存对象收集器

1.新生代GC(Minor GC):指发生在新生代的垃圾收集动作,Minor GC非常频繁,一般回收速度也比较快.

2.老年代GC(Major GC/Full GC):指发生在老年代的GC,出现了Major GC,经常会伴随至少一次的Minor GC,Major GC的速度一般会比Minor GC慢10倍以上.

6.虚拟机性能监控与故障处理工具

• jps:虚拟机进程状况工具
• jstat:虚拟机统计信息监视工具
• jinfo:Java配置信息工具(实时地查看和调整虚拟机各项参数)
• jmap:Java内存映像工具
• jhat:虚拟机堆转储快照分析工具
• jstack:Java堆栈跟踪工具
• JConsole和VisualVM(可视化工具)

7.虚拟机执行子系统

IV和WOE记录

IV （Information Value）

1）用途：评价特征或变量的预测能力。类似的指标还有信息增益 、增益率和基尼系数等

2）IV的计算依赖于WOE

WOE（Weight of Evidence）

1）要对一个变量进行WOE编码，需要把这个变量进行分组处理（离散化 / 分箱），分组后对于第i组，WOE的计算公式如下：

其中，$py_i$是这个组中响应客户占所有样本中响应客户的比例，$pn_i$是这个组中未响应客户占样本中未响应客户的比例。

所以，WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和”当前分组中没有响应的客户占所有没响应的客户的比例“的差异

IV的计算

其中，n为变量分组的个数。

为什么使用IV而不是直接用WOE

• 1.IV和WOE的差别在于IV在WOE基础上乘以（$py_i-pn_i$）- $pyn$ ,乘以了这个$pyn$变量保证了每个分组的结果都是非负数。
• 2.乘以$pyn$后，体现出了变量当前分组中个体的数量占整体个体数量的比例，对变量预测能力的影响。

IV的极端情况处理

• 1.合理分组
• 2.0 —> 1

这是一个基本概念,且很重要,记录一下.

树的定义:用图的知识来表示即为,无环的连通图或者边数等于顶点数减1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

package questionCheckisTree;
import java.util.Scanner;
/**
 * Created by duncan on 17-7-30.
 */
//本题为判断一个无向图是否是一颗树
    //树为无环的连通图或者边数等于顶点数-1
class Graph{
    //邻接矩阵,从1开始存储
    int[][] graph = new int[501][501];
    //顶点数和边数
    int nodes,edges;
}
public class Main {
    //判断是否是连通图,并且顶点数-1是否是边数
    //判断是否是连通图深度遍历一遍,都遍历到了即为连通图
    public void DFS(int[] visited,Graph graph,int start){
        //如果该顶点没有访问过
        if(visited[start] == 0){
            visited[start] = 1;
            //继续访问与其相连的顶点
            for(int i = 1; i <= graph.nodes; i++){
                if(graph.graph[start][i] == 1)
                    DFS(visited,graph,i);
            }
        }
    }
    public static void main(String[] args) {
        Main solution = new Main();
        Scanner in = new Scanner(System.in);
        int num = in.nextInt();
        for(int i = 0; i < num; i++){
            //输入顶点数和边数
            Graph graph = new Graph();
            graph.nodes = in.nextInt();
            graph.edges = in.nextInt();
            //初始化邻接矩阵
            for(int j = 0; j < graph.edges; j++){
                int a = in.nextInt();
                int b = in.nextInt();
                graph.graph[a][b] = 1;
                graph.graph[b][a] = 1;
            }
            if(graph.edges != graph.nodes - 1)
            {
                System.out.println("NO");
                continue;
            }
            //判断是否连通
            //初始化一个顶点访问数组,从1开始存储
            int[] visited = new int[graph.nodes+1];
            solution.DFS(visited,graph,1);
            //对visited数组判断
            boolean flag = true;
            for(int j = 1; j < graph.nodes; j++) {
                if (visited[j] == 0) {
                    flag = false;
                    break;
                }
            }
            if(flag)
                System.out.println("YES");
            else
                System.out.println("NO");
        }
    }
}

表达式求值

对于表达式的求值,一般使用中缀表达式转后缀表达式后,对后缀表达式求值,因为对于后缀或者前缀表达式计算,计算的顺序都是唯一的.

中缀表达式转后缀表达式的方法：

• 1.遇到操作数：直接输出（添加到后缀表达式中）
• 2.栈为空时，遇到运算符，直接入栈
• 3.遇到左括号：将其入栈
• 4.遇到右括号：执行出栈操作，并将出栈的元素输出，直到弹出栈的是左括号，左括号不输出。
• 5.遇到其他运算符：加减乘除：弹出所有优先级大于或者等于该运算符的栈顶元素，然后将该运算符入栈
• 6.最终将栈中的元素依次出栈，输出。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  public ArrayList<String> SuffixExpression(ArrayList<String> string){ ArrayList<String> suffix = new ArrayList<>(); Stack<String> stack = new Stack<>(); for(int i = 0; i < string.size(); i++){ if(string.get(i).equals("*") || string.get(i).equals("/") || string.get(i).equals("(")){ //push stack.push(string.get(i)); } else if(string.get(i).equals("+") || string.get(i).equals("-")){ while(!stack.isEmpty() && (stack.peek().equals("*") || stack.peek().equals("/"))) { suffix.add(stack.pop()); } //push stack.push(string.get(i)); } else if(string.get(i).equals(")")) { while(!stack.isEmpty() && !stack.peek().equals("(")) suffix.add(stack.pop()); //pop ( stack.pop(); }else{ suffix.add(string.get(i)); } } //push all elements in stack while(!stack.isEmpty()) suffix.add(stack.pop()); return suffix; }

计算后缀表达式

遇到操作数压入栈,否则弹出两个操作数进行操作后再压入栈中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

public int CalaculateSuffix(ArrayList<String> suffix){
        //when meet operator, pop two elements to calaculate
        Stack<String> stack = new Stack<>();
        for(int i = 0; i < suffix.size(); i++){
            if(!(suffix.get(i).equals("+") || suffix.get(i).equals("-") || suffix.get(i).equals("*") || suffix.get(i).equals("/")))
                //push into stack
                stack.push(suffix.get(i));
            else{
                //calucate
                String operator = suffix.get(i);
                String b = stack.pop();
                String a = stack.pop();
                String temp = String.valueOf(operate(a,b,operator));
                stack.push(temp);
            }
        }
        return Integer.valueOf(stack.pop());
    }

论文题目

Exploring Folksonomy for Personalized Search

概念解释

Folksonomy:

该单词由folk和taxonomy组成，folk是口语中伙伴的意思，taxonomy是分类方法的意思，该词用来表示现在存在的大众分类的一种现象。目前许多应用允许用户上传资源时选择标签标注该资源。现有的应用如flickr和dogear。

Motivation

对于这样允许大众分类的应用，如何满足用户在搜索时尽可能准确地返回用户所需要的资源是一个有意思的问题。因为如果像传统的搜索方法仅通过查询关键词去匹配搜索结果，返回的结果可能会不满足用户的初衷。而且，不同的用户在搜索不同的资源时有可能会使用同样的关键词，比如，爱好运动和爱好喝咖啡的用户在搜索杯子的时候使用的关键词都可能是“杯子”，而返回的结果对于爱好运动的用户来说应该尽可能是运动型杯子，对于爱好喝咖啡的用户来说应该尽可能是咖啡杯子。所以，这里的问题都归结于Personalized Search。

Solution

根据之前的工作，解决这样问题的方法有两类:Query Refinement和Result Processing

1)对于查询术语进行替换和扩展，替换成其他的术语或者用其他的术语来填充
2)对查询返回的结果再排序或者结果聚类等方法
使用较为普遍的是Result Processing，该篇论文中使用的也是第二种方法。

本文中提出的方法分为三个步骤：
1)Query中的terms先求结果排序得到Ranklist
2)通过User的Interest Vector和资源的Topic Vector求相似性得到Ranklist
3)聚合两个list得到最终的Ranklist
(具体在实验过程中，为了提高效率，第二步求Ranklist只对第一步中的前N个再去求排序)

Details-Of-Methods

Step1：
对于Query中的terms去求资源排序，本文中采用BM25和Language Model for IR(LMIR)这两种文本检索模型。
先通过基本的文本检索去得到第一步的Ranklist。

Step2：
第二步是本文的核心。关键在于建立Topic Space,因为建立了Topic Space后，才能对用户建立兴趣向量，才能对资源建立主题向量，然后再去计算两者之间的相似性。

1.本文中的主题空间使用了Folksonomy的方法，以标注的tag作为向量的每一维，每个维的值的计算方法可以通过tfidf或者BM25来计算，从而构成用户和资源的兴趣和topic向量。
此外，本文中以ODP分好类的web pages的topic space作为baseline方法。

2.当分别构建好用户和资源的向量后，本文通过类PageRank算法来迭代形成最终的用户和资源的矩阵。R矩阵行代表用户，列代表兴趣。T矩阵行代表资源，列代表topic。

Step3：
本文中聚合两个list的方法是通过简单的WBF方法去得到最终的Ranklist

Evaluation-Methods

本文基于一个假设：用户收藏过或标注过的资源即为用户相关资源，以此来通过检索评价标准来评价Personalized Search。

数据挖掘整理

1.数据的基本描述

1.1 中心趋势度量

• 均值
• 截尾均值：丢弃高低端极端值后的均值
• 中位数：有序数据值得中间值
• 众数：集合中出现最频繁的值
• 中列数：最大值和最小值的平均值

1.2 数据散布

• 极差：最大值与最小值之差

• 分位数：取自数据分布的每隔一定间隔上的点，把数据划分成基本上大小相等的连贯集合

• 四分位数：3个数据点，把数据分布划分成4个相等的部分，使得每部分表示数据分布的四分之一。（中位数、四分位数、百分位数是使用广泛的分位数）

• 方差

• 标准差

• 四分位数极差（IQR）：第1个和第3个四分位数之间的距离，IQR = Q3 - Q1

  识别可疑的离群点的通畅规则是，挑选落在第3个四分位数之上或第一个四分位数之下至少1.5*IQR处的值。

  ---

  图形的表示

  ---

• a)盒图：盒的端点一般在四分位数上，使得盒的长度是四分位数极差IQR。中位数用盒内的线标记。盒外的两条线延伸到最小和最大观测值。

• b)分位数图：一种观察单变量数据分布的简单有效方法

• c)直方图：

• d)散点图：确定两个数值变量之间看上去是否存在联系、模式或趋势的最有效的图形方法之一

1.3 相似性的度量

• Jaccard相似性
• 余弦相似性
• 欧式距离、曼哈顿距离、闵可夫斯基距离

2.数据预处理

2.1数据清洗：填写缺失值、光滑噪声数据，识别或删除离群点，并解决不一致性来“清理”数据

• 缺失值的处理：忽略该行、人工填写缺失值、使用一个全局常量填充、使用属性的中心度量（均值或中位数）、使用与给定元组属同一类的所有样本的均值或中位数、使用最可能的值填充缺失值（使用回归、使用贝叶斯形式方法的基于推理的工具或决策树归纳确定）

2.2数据集成：分析中的数据来自多个数据源

• 冗余和相关性分析：标称数据的卡方相关检验、Pearson相关系数、协方差

2.3数据归约：维归约和数值归约

2.4数据变换：

• 光滑：去掉噪声
• 属性构造：可以由给定的属性构造新的属性并添加到属性集中
• 聚集：对数据进行汇总或聚集
• 规范化：把属性数据按比例缩放
• 离散化：label encoder 、onehot
• 由标称数据产生概念分层：属性层级划分

准确率和召回率的计算

准确率是预测正确数量 / 总数量

精确率(precision)是针对预测结果而言,它表示的是预测为正的样本中有多少是真正的正样本.预测为正有两种可能,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),P = TP / (TP + FP)

召回率(recall)是针对原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。那也有两种可能，一种是把原来的正类预测成正类(TP)，另一种就是把原来的正类预测为负类(FN)。R = TP / (TP + FN)

精确率 = 提取出的正确信息条数 / 提取出的信息条数
召回率 = 提取出的正确信息条数 / 样本中的信息条数

举这样一个例子：某池塘有1400条鲤鱼，300只虾，300只鳖。现在以捕鲤鱼为目的。撒一大网，逮着了700条鲤鱼，200只虾，100只鳖。那么，这些指标分别如下： 正确率 = 700 / (700 + 200 + 100) = 70% 召回率 = 700 / 1400 = 50% F值 = 70% \* 50% \* 2 / (70% + 50%) = 58.3%

F值 = 精确率 * 召回率 * 2 / (精确率 + 召回率)

对于多分类或者n个二分类混淆矩阵上综合考察查准率(precision)和查全率(recall)
1.一种直接的做法是现在各混淆矩阵上分别计算出查准率和查全率,记为(P1,R1),…,(Pn,Rn),再计算平均值,这样就得到”宏查全率”(macro-P),”宏查全率”(macro-R),以及相应的”宏F1”(macro-F1):
\(macro-P = \frac{1}{n}\sum_{i=1}^{n}Pi\)

\(macro-R=\frac{1}{n}\sum_{i=1}^{n}Ri\)

\(macro-F1=\frac{2*macro-P*macro-R}{macro-P+macro-R}\)

2.还可先将各混淆矩阵对应元素进行平均,得到TP/FP/TN/FN的平均值,分别记为ATP,AFP,ATN,AFN,再基于这些平均值计算出”微查准率(micro-P)”/“微查全率”(micro-R)和”微F1”(micro-F1):
\(micro-P = \frac{ATP}{ATP + AFP}\)

\(micro-R=\frac{ATP}{ATP + AFN}\)

\(micro-F1=\frac{2*micro-P*micro-R}{micro-P+micro-R}\)

如何提高准确率

提高准确率的手段可以分为三种:1)Bagging 2)Boosting 3)随即森林

在一般经验中,如果把好坏不等的东西掺到一起,那么通常结果会是比最坏的要好一些,比最好的要坏一些.集成学习把多个学习器结合起来,如何能够获得比最好的单一学习器更好的性能呢?

要获得好的集成,个体学习器应”好而不同”,即个体学习器要有一定的”准确性”,即学习器不能太坏,并且要有”多样性”,即学习器间具有差异.
目前的集成学习方法大致分为两大类:个体学习器间存在强依赖关系,必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系,可同时生成的并行化方法;前者的代表是Boosting,后者的代表是Bagging和”随机森林”.
Boosting最著名的代表是AdaBoost.

BackTracking Algorithm Notes

1.定义

在那些涉及寻找一组解的问题或者求满足某些约束条件的最优解的问题中，有许多问题可以用回溯法来求解。

为了应用回溯法，所要求的解必须能表示成一个n-元组（x1,x2,…,xn）,其中xi是取自某个有穷集Si。通常，所求解的问题需要求取一个使某一规范函数P(x1,…,xn)取极大值（或取极小值或满足该规范函数条件）的向量。有时还要找出满足规范函数P的所有向量。

2.基本思想

不断地用修改过的规范函数（或限界函数）Pi(x1,…,xn)去测试正在构造中的n-元组的部分向量(x1,…,xn)，看其是否可能导致最优解，如果不能，那么将可能要测试的其余向量略去，就是剪枝。

约束条件分为两类：显式约束和隐式约束。显示约束是限定每个x只从一个给定的集合上取值。隐式约束描述了xi必须彼此相关的情况，规定解空间中那些实际上满足规范函数的元组。

1
2
3
4
5
6
7
8
9
10
11
12

Algorithm backTracking
procedure PBACKTRACK(k)
//此算法是对回溯法抽象地递归描述。进入算法时，解向量X(1:n)的前k-1个分量X(1),...,X(k-1)已赋值
	global n,X(1:n)
	for 满足下式的每个X(k)
		X(k) 属于 T(X(1),...,X(k-1)) and B(X(1),...,X(k)) = True do
		if (X(1),...,X(k)) 是一条已抵达答案结点的路径 then
			print (X(1),...,X(k))
		endif
	call PBACKTRACK(k + 1)
	repeat
end PBACKTRACK

3.代表性的问题

a、n-queen问题

有关n后问题的定义自行查阅，这里不给出解释。

解决思路
假定皇后i将放在行i上，因此，8皇后问题可以表示出8-元组(x1,x2,…,x8)，其中xi是放置皇后i所在的列号。隐式约束条件：1）没有两个xi可以相同；2）没有两个皇后可以在同一条对角线
假设两个皇后在(i,j)和(k,l)位置，则在同在对角线公式为abs(j-l) = abs(i-k)。即，在PLACE函数中可用此公式来判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

procedure NQ(k)
//X(1),...,X(k-1)已赋值，求X(k),...,X(n)
	global X(1:n)
	X(k) = 1
	while X(k) <= n do
	//PLACE为检测第k个皇后是否满足约束条件
		if PLACE(k) then
			if k = n then 
				print (X(1),...,X(n))
			else
			//继续生成
				NQ(k + 1)
			endif
		endif
		X(k) = X(k) + 1
	repeat
end NQ

b、子集和数问题

定义：已知n+1个正数：Wi,1<=i<=n和M。要求找出Wi的和数为M的所有子集。例如，若n=4，(W1,W2,W3,W4)=(11,13,24,7),M=31，则满足要求的子集是(11,13,7)和(24,7)。值得指出的是，通过给出其和数为M的那些Wi的下标来表示解向量比直接用这些Wi表示解向量更为方便。因此这个解向量由(1,2,4)和(3,4)表示。

显示约束条件要求Xi在1~n之间。隐式约束条件则是要求没有两个Xi是相同的且相应的Wi的和数是M。(为了避免产生同一个子集重复的情况,如(1,4,2)和(1,2,4))，附加另一个隐式约束条件:Xi+1大于Xi,i在1~n之间。

解决思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//current代表当前集合中已有和，k表示当前判断的第k个元素，rest代表集合中剩余元素之和
public void sumOfsubset(int current,int k,int rest){
    //先生成左儿子,w[k]加入
    flag[k] = 1;
    if(current + w[k] == M){
        System.out.print("{\t");
        //子集找到，输出
        print(k);
        System.out.println();
    }
    else if(current + w[k] + w[k + 1] <= M)
        sumOfsubset(current + w[k],k + 1,rest - w[k]);
    //生成右儿子,w[k]不加入
    if((current + rest - w[k] >= M) && (current + w[k + 1] <= M)){
        flag[k] = 0;
        sumOfsubset(current,k + 1,rest - w[k]);
    }
}

c、图的着色

定义：已知一个图G和m>0种颜色，在只准使用这m种颜色对G的结点着色的情况下，是否能使图中任何相邻的两个结点都具有不同的颜色。这个问题称为m-着色判定问题。

解决思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

   	procedure MCOLORING(k)
	global integer m,n,X(1:n),boolean Graph(1:n,1:n)
	integer k
	loop
		//给第k个结点赋值颜色
		call NextValue(k)
		if X(k) = 0 then
			exit
		endif
		if k = n then
			print(X)
		else
			call MCOLORING(k + 1)
		endif
	repeat
end MCOLORING

d、哈密顿环

定义：一个哈密顿环是一条沿着图G的n条边环行的路径，它访问每个结点一次并且返回到它的开始位置。

e、0/1背包问题

定义不解释，这个问题解决的方案很多，可以用动归、贪心算法，这里使用回溯法求解。
代码如下：

解决思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

package Chapter8;
//Created by duncan on 16-12-14.
public class BPByBackTrack {
    int bestvalue = 0;
    int[] lastfalg;
    public void swap(int[] x,int m,int n){
        int temp;
        temp = x[m];
        x[m] = x[n];
        x[n] = temp;
    }
    //先将物品效益和重量按照P/W的大小非递减排序,p和w都从1开始存储
    public void sort(int[] p,int[] w){
        int len = p.length -1 ;
        for(int i = 1; i <= len; i++){
            for(int j = 1; j <= len - i; j++){
                    if(((float)p[j] / w[j]) > ((float)p[j + 1] / w[j + 1])){
                        swap(p,j,j + 1);
                        swap(w,j,j + 1);
                    }
            }
        }
    }
    //限界函数,k为上次去掉的物品，M为背包容量,currentp为当前背包中效益值，currentw为背包中当前重量，返回值为当前最大值上限
    public int Bound(int[] p,int[] w,int k,int M,int currentp,int currentw){
        int tempp = currentp,tempw = currentw;
        int len = p.length - 1;
        for(int i = k + 1; i <= len; i++){
            tempw += w[i];
            if(tempw < M)
                tempp += p[i];
            else
                return (tempp + (1 - (tempw - M) / w[i] * p[i]));
        }
        return tempp;
    }
    //回溯法求解背包问题,p,w为效益值和重量数组，M为背包容量，k为当前处理的物品，flag为记录物品放或不放的标志数组,currentp为当前效益，currentw为当前重量
    public void BKNAPBT(int[] p, int[] w,int M,int k,int[] flag,int currentp,int currentw){
        int n = p.length - 1;
        if(k > n){
                if(currentp > bestvalue) {
                    bestvalue = currentp;
                    lastfalg = flag.clone();
                    return;
                }
        }
        else{
            //进入左子树
            if(currentw + w[k] <= M)
            {
                flag[k] = 1;
                BKNAPBT(p,w,M,k + 1,flag,currentp + p[k],w[k] + currentw);
            }
            //进入右子树前先判断右子树的最大上限是否能够比当前最优值大，如果没有则减去右子树
            if(Bound(p,w,k,M,currentp,currentw) >= currentp) {
                flag[k] = 0;
                BKNAPBT(p, w, M, k + 1, flag, currentp, currentw);
            }
        }
    }
    public void print(int[] p, int[] w){
        int len = p.length -1;
        int m = 0,v = 0;
        System.out.println("\n最终放入背包的物品的价值为:");
        for(int i = 1; i <= len; i++){
            if(lastfalg[i] == 1) {
                m += w[i];
                v += p[i];
                System.out.print(p[i] + " ");
            }
        }
        System.out.println("\n\n最终重量为：" + m);
        System.out.println("\n最优解价值为:" + v);
    }
    public static void main(String[] args) {
        int m = 0,M = 110;
        BPByBackTrack bp = new BPByBackTrack();
        int[] w = {0,1,11,21,23,33,43,45,55};
        int[] p = {0,11,21,31,33,43,53,55,65};
        int[] flag = {0,0,0,0,0,0,0,0,0};
        System.out.println("物品价值为");
        for(int i = 1 ; i <= p.length -1 ;i++){
            System.out.print(p[i] + "\t");
        }
        System.out.println("\n物品重量为");
        for(int i = 1 ; i <= p.length -1 ;i++){
            System.out.print(w[i] + "\t");
        }
        System.out.println();
        bp.sort(p,w);
        bp.BKNAPBT(p,w,M,1,flag,0,0);
        System.out.println("背包容量为:" + M);
        bp.print(p,w);
    }
}

简要

本篇主要记录三种求最优解的算法:动态规划(dynamic programming),贪心算法和平摊分析.

动态规划

1.动态规划是通过组合子问题的解而解决整个问题的.分治法算法是指将问题划分成一些独立的子问题, 递归地求解各个子问题,然后合并子问题的解而得到原问题的解.与此不同,动态规划适用于子问题不是独立的情况,也就是各个子问题包含公共的子子问题.在这种情况下,若用分治法则会做许多不必要的工作,即重复地求解公共的子子问题.

动态规划算法的设计可以分为以下四个步骤:

1.描述最优解的结构
2.递归定义最优解的值
3.按自底向上的方式计算最优解的值
4.由计算出的结果构造一个最优解

能否运用动态规划方法的标志之一:一个问题的最优解包含了子问题的一个最优解.这个性质为最优子结构.

适合采用动态规划的最优化问题的两个要素:最优子结构和重叠子问题

贪心算法

1.贪心算法是使所做的选择看起来都是当前最佳的,期望通过所做的局部最优选择来产生出一个全局最优解.

2.贪心算法的每一次操作都对结果产生直接影响,而动态规划不是.贪心算法对每个子问题的解决方案做出选择,不能回退;动态规划则会根据之前的选择结果对当前进行选择,有回退功能.动态规划主要运用于二维或三维问题,而贪心一般是一维问题.

3.贪心算法要经过证明才能运用到算法中.

平摊分析

(未完-待续)

金融建模比赛记录

数据处理

对于A训练集（有标签）:

• 1.数据分散在四个文件内,train_behavior,train_ccx,train_consumer,train_target,各个数据文件的解释大赛excel表格中已有.
• 2.需要根据ccx_id将每个文件中的数据进行聚合, 聚合之前可以先在每个文件中提取特征.
• 对于每个文件内

• train_behavior（基础信息+行为数据）:一共2270维特征，对其中(1)唯一值列去除—共去除23列;（2）对于缺失90%值的列进行去除;(3)对于包含空值且只有两种值的列进行去除;(类别值的列:’var3’, u’var4’, u’var5’, u’var6’, u’var11’, u’var12’, u’var13’, u’var14’, u’var15’, u’var18’, u’var19)。最终得到336维特征(3)去除时间列(2列)
• train_consumer(消费数据): 用户的消费记录,提取了\
• train_ccx(查询记录)：用户的查询记录,提取了”查询次数”以及categorical列的次数

初步结果(模型都是默认参数)

对于B训练集(无标签)

该问题属于半监督学习,半监督学习分为纯半监督学习和直推学习.

• 纯半监督学习:是将未标记数据和有标记数据都作为训练集来训练,得到模型,来预测待测数据
• 直推学习:是将未标记数据作为需要预测的对象,通过有标记数据进行训练,来预测.

解决思路:

• 1.聚类将A和B合并聚为两类,用该聚类簇中A标签投票标记B(否决)
• 2.自训练方法,先训练A得到一个分类模型,然后通过分类模型分类B,将置信度高的进行标记,然后加入训练集,训练->标记置信度高的,迭代.(尝试)